|
Huvi maagiliste ruutude vastu on viimastel aastatel suurenenud.
Interneti rubriigis Magic Square käsitletakse seda
teemat (1997. aasta lõpul) enam kui 1500 uurimuses ja kirjutises.
Loodetakse, et maagiliste ruutude koostamisel kasutatavatest
meetoditest võib kasu olla automaatika probleemide lahendamisel.
Internetist
saame ka teada, et peetakse arvestust suurimate maagiliste
ruutude koostamise kohta ja seda kahes võistlusliigis.
- Lahendused
arvuti abil; arvutiga koostatud maagilistest ruutudest on
senini suurim 3001 x 3001 (rekord 1994. aastast).
- Lahendused
käsitsi; senine suurim on 1111 x 1111 (rekord
1990. aastast).
Olgu märgitud,
et maagiliste ruutude lahendamise metoodikaga tegeles juba
tulemuslikult tuntud teadusmees Benjamin Franklin (Letters
and papers on Philosophical subjects by Benjamin Franklin,
LL.D., F.R.S., London, 1769).
Maagilistest ruutudest kavatseb Horisont avaldada materjale
järgnevates numbrites.
Eesti Entsüklopeediast loeme, et maagiline ruut koosneb
n reast ja n veerust ning nendesse ridadesse ja veergudesse
on paigutatud naturaalarvud 1, 2, 3, ... n² nii, et igas reas,
veerus ja kummaski diagonaalis asetsevate arvude summa on
ühesugune. Seda summat nimetatakse vastava ruudu maagiliseks
konstandiks ja selle saab määrata valemiga
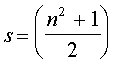
Kirjeldatud
ruutu nimetatakse ka n-järku maagiliseks ruuduks (maatriksiks).
Neljandat
järku maagilise ruudu üks variant on esitatud EE ülalmainitud
artiklis (joonis 1):

Joonis 1
Selle
ruudu maagiline konstant on
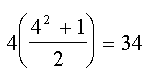
Neljandat
järku maagilise ruudu teise variandi leiame mitmesuguste tehnikaprobleemide
lahendamiseks laialdaselt kasutatava programmipaketi MATLAB
üldjuhendist The MATLAB EXPO (joonis 2):

Joonis 2
Maagilise
ruudu vaadeldava variandi autoriks peetakse kuulsat saksa
maalikunstnikku ja harrastusmatemaatikut Albrecht Dürerit,
kes selle on esitanud oma gravüüril Melanhoolia I.
Maagilise ruudu alumisse ritta on A. Dürer kirjutanud gravüüri
loomise aasta, 1514.
Nii nagu
paljudele ristsõna lahendamine, võib mõnele ka maagiliste
ruutudega tegelemine pakkuda mõnusat ajaviidet. Ja kui lahendus
käes, siis hüüdke alla tänavale (parafraseerides Mihkel
Vesket): Ilus oled, matemaatika!
Pakume
puremiseks viiendat järku maagilise ruudu, mille konstant
on
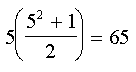
Vähemalt
ühel lahendusvariandil on keskmise rea ja keskmise veeru lõikeruudus
arv 13 (joonis 3). Olgu märgitud, et lahendusvariante
on kaugelt rohkem kui üks.
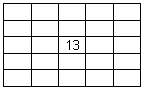
Joonis 3
Ülesande
lahendamiseks on mitu meetodit (vt. L. Väljaots, Ü. Kaasik.
Maagilised ruudud. Matemaatika ja kaasaeg XVII. Tartu
1970), sealhulgas terrasside meetod ja ääristamismeetod. Ned
mõlemad on rakendatavad paarituarvuliste n-järku maagiliste
ruutude puhul.
Terrasside
meetod annab tulemuse kätte vähese ajakuluga, kuid seejuures
saadakse võimalikest lahendustest ainult üks variant —
üks maagiline ruut.
Olgu siinkohal
märgitud, et iga lähteruudu pöörete ja peegelduste tulemusena
saadakse otsekohe (formaalselt) veel seitse maagilist ruutu.
Terrasside
meetodi rakendamise kirjeldus L. Väljaotsa, Ü. Kaasiku
artikli järgi on järgmine. Selle meetodi puhul täiendatakse
koostatav ruut kõigepealt sümmeetrilisteks trepikujuliste
äärtega kujundiks, nagu viiendat järku ruudu jaoks on näidatud
joonisel 4. Saadud kujundisse paigutatakse mööda diagonaale
järjekorras arvud 1,2,…, n². Näiteks joonisel 4 on seda
tehtud vasakult alt üles paremale kulgevaid diagonaale pidi.
Osa arve (3, 9, 15, 8 jne.) satuvad sellise paigutamise korral
juba ruudu lahtritesse õigetele kohtadele, muist arve (1,
2, 4, 5, 6, 10 jne.) jääb aga väljapoole ruutu

Joonis 4
Need
väljapoole jäänud arvud tõstame nüüd n (näite puhul viie)
koha võrra ruudu suunas mööda seda rida või veergu, millel
nad paiknevad. Nii valmibki maagiline ruut (maagilise konstandiga
s = 65), mis antud näite jaoks on esitatud joonisel
5.
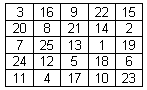
Joonis 5
Võimalike
viiendat järku maagiliste ruutude üldarv ei ole teada. On
teada ainult kolmandat ja neljandat järku maagiliste ruutude
üldarv. Need arvud on vastsvalt 8 ja 880 (eelnimetatud L. Väljaotsa,
Ü. Kaasiku artikli andmetel). Ilmselt on viiendat järku
maagiliste ruutude arv suurem.
Riiskade
meetod võimaldab (n – 2)-järku maagilisest ruudust
lähtudes konstrueerida n-järku maagilise ruudu. Seega viiendat
järku maagilise ruudu konstrueerimisel tuleb lähtuda kolmandat
järku maagilisest ruudust, näiteks joonisel 6 näidatud ruudust.

Joonis 6
See ruut
on sihilikult valitud iseäralikuna, mis seisneb selles, et
kõigil tema ridadel, veergudel ja mõlemal peadiagonaalil on
ühesugune summa, s.o. 39.
Eelöeldut
silmas pidades lihtsustub oluliselt viiendat järku maagilise
ruudu konstrueerimine. Nimelt tuleb kolmandat järku ruudu
(joonis 6) iga rida, veergu ja peadiagonaali täiendada kahe
arvuga, mille summa on 26 (sest s = 65 = 39 + 26).
Vajalik arvupaar (nn. riisk e. koba) tuleb valida joonisel
7 näidatud järjestusest.
1
— 25
2
— 24
.
. .
.
. .
11
— 15
12
— 14
13
Joonis 7
Lähteruudu
(joon. 6) konstrueerimiseks on sellest järjestusest juba höivatud
riisad 8-18, 10-16, 11-15 ja 12-14.
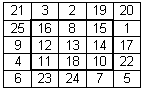
Joonis 8
Joonisel
8 on näidatud ülejäänud riiskade paigutus lähteruudu ümber.
Tulemuseks on viiendat järku maagiline ruut (joonis 8). Selle
ruudu abil võib saada uusi ruute, paigutades riisku 3 — 23,
2 — 24 ja 7 — 19 omavahel ümber.
Samuti saab uusi maagilisi ruute, talitades analoogiliselt
riiskadega 1 — 25, 9 — 17 ja 4 — 22.
Kui
selliselt saadud maagilistele ruutudele rakendatakse pöördeid
ja peegeldusi, suureneb maagiliste ruutude arv veel seitsmekordselt.

Joonis 9
Valides
aluseks mõne teise kolmandat järku ruudu (näiteks tugeva joonega
ümbritsetud südamik joonisel 9) ja rakendades eespool käsitletud
metoodikat, saadakse joonisel 9 esitatud viiendat järku maagiline
ruut. Selle ruudu alusel uute maagiliste ruutude saamine on
analoogiline joonise 8 kohta öelduga.
Vaadeldud
metoodika on kasutatav kõikide paarituarvulise n-järku maagiliste
ruutude konstrueerimiseks.

Näiteks
seitsmendat järku maagilise ruudu puhul (maagiline konstant
s = 175) võib aluseks võtta joonisel 10 näidatud
kolmandat järku ruudu, mille keskmises lahtris on arv 25 ja
riiskade väärtus on 50. Vajalik riisk tuleb valida joonisel
11 näidatud järjestusest.
1
— 49
2
— 48
.
. .
.
. .
23
— 27
24
— 26
25
Joonis
11
Samast
järjestusest valitud riiskadega haaratakse joonisel 10 näidatud
ruut ja saadakse viiendat järku maagiline ruut, mida omakorda
haaratakse mainitud järjestuse ülejäänud riiskadega. Tulemuseks
on seitsmendat järku maagiline ruut (joonis 12).
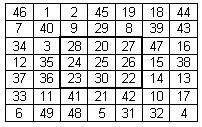
Joonis 12
Olgu
märgitud, et riisad ei tarvitse sattuda kohe esimesel katsel
õigetesse kohtadesse. Neid tuleb vajadusel ümber tõsta selleks,
et saada maagilise ruudu esimese ja teise ning viimase ja
eelviimase rea, aga samuti esimese ja teise ning viimase ja
eelviimase veeru nõutavate summade väärtusi. Seejuures riiskade
väärtusi ei muudeta.
Tundub,
et ülalesitatud riiskade meetodi käsitluses on mõningaid uusi
mõtteid, näiteks maagilise ruudu konstrueerimine riiskade
abil.
tagasi ...
|